2つの動点がn回の移動で重なる確率

点Aと点B上にそれぞれ動点XとYが最初存在する。X，Yは「現在いる点と結ばれている線分を等確率で選んで他点に移動する」試行を交互に行い、２点が重なったら終了する。合計n回試行し終了する確率P(n)を求めよ。http://bit.ly/exCQHw (nyoki1007様)

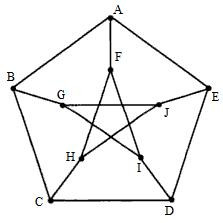
10 点全て、以下の 2 つの性質を満たす。
・距離 1 の点 3 つの間に経路はない
・距離 2 の点 6 つは距離 1 への経路を 1 つずつ持つ

よって、X と Y がどこにいてどちらが動く場合でも、
・現在距離が 1 ならば確率 1/3 で重なり、確率 2/3 で距離 2 になる
・現在距離が 2 ならば確率 1/3 で距離 1 になり、確率 2/3 で距離 2 のまま
である。

つまり、n 回試行後に距離 1 である確率を Q_n, 距離 2 である確率を R_n とすると、
Q_(n+1) = 1/3 R_n
R_(n+1) = 2/3 Q_n + 2/3 R_n

これから Q_n を消去すると、
R_(n+2) = 2/3 R_(n+1) + 2/9 R_n

α, β = (1±√3)/3 とすると、

R_(n+2) - αR_(n+1) = β( R_(n+1) - αR_n )
R_(n+2) - βR_(n+1) = α( R_(n+1) - βR_n )
また、R_0 = 0, R_1 = 2/3

よって、
R_(n+1) - αR_n = 2/3 β^n
R_(n+1) - βR_n = 2/3 α^n

したがって、R_n = 2/3 (α^n-β^n)/(α-β)

n (≧2) 回目に試行が終了するためには n-2 回時点で距離 2 で、
そこから互いに近づけばよい。
したがって P_n = 2/27 (α^(n-2)-β^(n-2))/(α-β)

P_1 = 1/3 であるからこの式は n=1 のときも含んでいる。

よって α, β を代入して、
P_n = √3/27 ( ((1+√3)/3)^(n-2) - ((1-√3)/3)^(n-2) )